Matrix Class Reference

Matrix type. More...

#include <matrix.h>

Inherits Storeable.

Collaboration diagram for Matrix:
Collaboration graph
[legend]

List of all members.

Public Member Functions

 Matrix ()
 default constructor: zero matrix (0x0)
 Matrix (I _m, I _n, const D *_data=0)
 constucts a matrix with the given size.
 Matrix (I _m, I _n, D def)
 constucts a matrix with the given size and fills it with the default value
 Matrix (const Matrix &c)
 constucts a instance on the base of a deep copy of the given matrix
 ~Matrix ()
I getM () const
I getN () const
I size () const
D val (I i, I j) const
D & val (I i, I j)
D valDef0 (I i, I j) const
void set (I _m, I _n, const D *_data=0)
 sets the size of the matrix and maybe the data if given (row-wise).
void set (const D *_data)
 sets the data (row-wise).
Matrix row (I index) const
Matrix rows (I startindex, I endindex) const
Matrix column (I index) const
Matrix columns (I startindex, I endindex) const
int convertToBuffer (D *buffer, I len) const
 stores the content of the matrix (row-wise) in the given buffer
std::list< D > convertToList () const
const double * unsafeGetData () const
 returns a pointer to the data. UNSAFE!!!
bool store (FILE *f) const
 stores the Matrix into the given file stream (binary)
bool restore (FILE *f)
 reads a Matrix from the given file stream (binary)
bool write (FILE *f) const
 writes the Matrix into the given file stream (ascii)
bool read (FILE *f)
 reads a Matrix from the given file stream (ascii)
void add (const Matrix &a, const Matrix &b)
 addition: this = a + b
void add (const Matrix &a, const D &summand)
void sub (const Matrix &a, const Matrix &b)
 add scalar to each element
void mult (const Matrix &a, const Matrix &b)
 multiplication: this = a * b
void mult (const Matrix &a, const D &fac)
 scaling: this = a * fac
void exp (const Matrix &a, int exponent)
 exponent, this = a^i,
bool isNulltimesNull () const
 returns true if matrix is a 0x0 matrix
bool isVector () const
 returns true if matrix is a vector
bool equals (const Matrix &a) const
 bytewise comparison (compares data buffer bytewise, which implies that n1*m1 == n2*m2 but not necessarily n1==n2)
Matrix pseudoInverse (const D &lambda=1e-8) const
 calculates the pseudoinverse, depending on the shape of the matrix the left or right pseudoinverse is used.
Matrix secureInverse () const
 calculates the secure inverse of a square matrix.
bool hasNormalEntries () const
 returns true if all entries are normal floating point numbers, otherwise false (e.g.
Matrix map (D(*fun)(D)) const
 maps the matrix to a new matrix with all elements mapped with the given function
Matrix mapP (D param, D(*fun)(D, D)) const
 like map but with additional double parameter for the mapping function (first argument of fun is parameter, the second is the value)
Matrix mapP (void *param, D(*fun)(void *, D)) const
 like map but with additional arbitrary parameter for the mapping function
Matrix multrowwise (const Matrix &factors) const
 row-wise multiplication
Matrix multcolwise (const Matrix &factors) const
 column-wise multiplication
Matrix multMT () const
 optimised multiplication of Matrix with its transposed: M * M^T
Matrix multTM () const
 optimised multiplication of transpsoed of Matrix with itself: M^T * M
D elementProduct () const
 returns the product of all elements (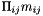$ \Pi_{ij} m_{ij} $)
D elementSum () const
 returns the sum of all elements (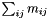$ \sum_{ij} m_{ij} $)
D norm_sqr () const
 returns the sum of all squares of all elements (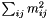$ \sum_{ij} m_{ij}^2 $) this is also known as the square of the Frobenius norm.
Matrix above (const Matrix &a) const
 returns a matrix that consists of this matrix above A (number of rows is getM + a.getM())
Matrix beside (const Matrix &a) const
 returns a matrix that consists of this left beside A (number of columns is getN + a.getN())
Matrix & operator= (const Matrix &c)
 deep copy
Matrix operator+ (const Matrix &sum) const
 sum of two matrices
Matrix operator- (const Matrix &sum) const
 difference of two matrices
Matrix operator* (const Matrix &fac) const
 matrix product
Matrix operator* (const D &fac) const
 product with scalar (D) (only right side)
Matrix operator^ (int exponent) const
 special matrix potence:
Matrix operator& (const Matrix &b) const
 row-wise multiplication
Matrix & operator+= (const Matrix &c)
 combined assigment operator (higher performance)
Matrix & operator-= (const Matrix &c)
 combined assigment operator (higher performance)
Matrix & operator*= (const Matrix &c)
 combined assigment operator (higher performance)
Matrix & operator*= (const D &fac)
 combined assigment operator (higher performance)
Matrix & operator&= (const Matrix &c)
 combined assigment operator (higher performance)
bool operator== (const Matrix &c) const
 comparison operator (compares elements with tolerance distance of COMPARE_EPS)
void copy (const Matrix &c)
 performs a deep copy of the given matrix
Matrix & toTranspose ()
 inplace transpose
Matrix & toZero ()
 inplace converts matrix to zero matrix
Matrix & toId ()
 inplace converts matrix to identity (use ^0 to get a copy version of it)
Matrix & toSum (const Matrix &a)
 inplace addition: this = this + a
Matrix & toSum (const D &sum)
 inplace addition: this = this + a, where a is a scalar
Matrix & toDiff (const Matrix &a)
 inplace subtraction: this = this - a
Matrix & toMult (const Matrix &a)
 inplace multiplication: this = this * a
Matrix & toMult (const D &fac)
 inplace multiplication with scalar: this = this*fac
Matrix & toExp (int exponent)
 special inplace matrix power:
Matrix & toMap (D(*fun)(D))
 inplace mapping of matrix elements (element-wise application)
Matrix & toMapP (D param, D(*fun)(D, D))
 like toMap, but with an extra double parameter for the mapping function.
Matrix & toMapP (void *param, D(*fun)(void *, D))
 like toMap, but with an extra arbitrary parameter for the mapping function.
Matrix & toMap2 (D(*fun)(D, D), const Matrix &b)
 like toMap, but with using 2 matrices
Matrix & toMap2P (D param, D(*fun)(D, D, D), const Matrix &b)
 like toMap2, but with additional parameter
Matrix & toMap2P (void *param, D(*fun)(void *, D, D), const Matrix &b)
 like toMap2P, but with arbitrary parameter
Matrix & toMultrowwise (const Matrix &factors)
 Inplace row-wise multiplication.
Matrix & toMultcolwise (const Matrix &factors)
 Inplace column-wise multiplication.
Matrix & toAbove (const Matrix &a)
 sets the matrix a below this matrix
Matrix & toBeside (const Matrix &a)
 sets the matrix a right beside this matrix
Matrix & toSort ()
 sorts the matrix (rowwise)
Matrix & reshape (I m, I n)
 reshapes the matrix without destroying the data.
Matrix & pluslambdaI (double lambda=1e-8)
 adds the given value to the diagonal
Matrix & addRows (I numberRows, const D *_data=0)
 adds one or more rows to the existing matrix and fills it with the given data
Matrix & addRows (I numberRows, const Matrix &dataMatrix)
 same as toAbove(dataMatrix)
Matrix & addColumns (I numberColumns, const D *_data=0)
 adds one or more columns to the existing matrix same as toBeside(Matrix(getM, numberColumns, _data))
Matrix & addColumns (I numberColumns, const Matrix &dataMatrix)
 same as toBeside(dataMatrix)
Matrix & removeRows (I numberRows)
 removes one or more rows of the existing matrix, same as reshape(getM()-numberRows, getN());
Matrix & removeColumns (I numberColumns)
 removes one or more columns of the existing matrix resets the size of the matrix and deletes the appropiate data.

Static Public Member Functions

static Matrix map2 (D(*fun)(D, D), const Matrix &a, const Matrix &b)
 binary map operator for matrices.
static Matrix map2P (D param, D(*fun)(D, D, D), const Matrix &a, const Matrix &b)
 like map2 but with additional parameter.
static Matrix map2P (void *param, D(*fun)(void *, D, D), const Matrix &a, const Matrix &b)
 like map2P but with arbitrary paramters (void*) instead of double

Friends

std::ostream & operator<< (std::ostream &, const Matrix &)
 printing operator: output format: mxn (
row0
..rown
) where rowX is tab seperated list of values

Detailed Description

Matrix type.

Type D is datatype of matrix elements, which is fixed to double. Type I is the indextype of matrix elements, which is fixed to unsigned int, if AVR is not defined. There are basicly two different types of operation: Inplace operations and copy operations. Please use the latter ones unless you know what you are doing. Just in case of critical performance optimisation use the inplace operations. The most convinient way is to use the overloaded operators (like + * ...). All constructed matrices are initialised with zero elements (unless data is given). All functions perform range checks if in debug mode (NDEBUG is not defined). Please use debug the version (default) for testing

See also:
examples/matrix/matrixexample.cpp
Author:
Georg Martius
Examples:

integration/main.cpp, and matrix/matrixexample.cpp.

Constructor & Destructor Documentation

Matrix (  )  [inline]

default constructor: zero matrix (0x0)

Matrix ( I  _m,
I  _n,
const D *  _data = 0 
)

constucts a matrix with the given size.

If _data is null then the matrix is filled with zeros. otherwise matrix will be filled with _data in a row-wise manner. In this case _data must be at least _m*_n elements long

Matrix ( I  _m,
I  _n,
D  def 
)

constucts a matrix with the given size and fills it with the default value

Matrix ( const Matrix &  c  ) 

constucts a instance on the base of a deep copy of the given matrix

~Matrix (  )  [inline]

Member Function Documentation

Matrix above ( const Matrix &  a  )  const

returns a matrix that consists of this matrix above A (number of rows is getM + a.getM())

returns a matrix that consists of b below this

void add ( const Matrix &  a,
const D &  summand 
)
void add ( const Matrix &  a,
const Matrix &  b 
)

addition: this = a + b

Matrix & addColumns ( I  numberColumns,
const Matrix &  dataMatrix 
)

same as toBeside(dataMatrix)

See also:
toBeside()
Parameters:
numberColumns number of columns to add (unused)
dataMatrix matrix which contains the data of the new rows
Returns:
the address of the matrix itself
Matrix & addColumns ( I  numberColumns,
const D *  _data = 0 
)

adds one or more columns to the existing matrix same as toBeside(Matrix(getM, numberColumns, _data))

See also:
toBeside()
Parameters:
numberColumns number of columns to add (this extends n)
_data data to add
Returns:
the address of the matrix itself
Matrix & addRows ( I  numberRows,
const Matrix &  dataMatrix 
)

same as toAbove(dataMatrix)

Parameters:
numberRows number of rows to add (unused)
dataMatrix matrix which contains the data of the new rows
Returns:
the address of the matrix itself
Matrix & addRows ( I  numberRows,
const D *  _data = 0 
)

adds one or more rows to the existing matrix and fills it with the given data

same as toAbove(Matrix(numberRows,getN(),data))

Parameters:
numberRows number of rows to add (this extends m)
_data data to add
Returns:
the address of the matrix itself
Matrix beside ( const Matrix &  a  )  const

returns a matrix that consists of this left beside A (number of columns is getN + a.getN())

returns a matrix that consists of b right beside this

Matrix column ( I  index  )  const
Returns:
column-vector(as Mx1 matrix) containing the index'th column
Examples:
matrix/matrixexample.cpp.
Matrix columns ( I  startindex,
I  endindex 
) const
Returns:
submatrix (as MxK matrix) containing column from startindex to endindex inclusively (K=endindex-startindex) indices can be out of bounds, they are clipped in any case
int convertToBuffer ( D *  buffer,
I  len 
) const

stores the content of the matrix (row-wise) in the given buffer

Parameters:
buffer Buffer for storing the elements (should have the length given by len)
len Length of the provided buffer. In any case only min(len, getM()*getN()) elements are copied.
Returns:
number of actually written elements
std::list< D > convertToList (  )  const
Returns:
a list of the content of the matrix (row-wise)
void copy ( const Matrix &  c  )  [inline]

performs a deep copy of the given matrix

D elementProduct (  )  const

returns the product of all elements (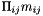$ \Pi_{ij} m_{ij} $)

returns the product of all elements

D elementSum (  )  const

returns the sum of all elements (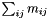$ \sum_{ij} m_{ij} $)

returns the sum of all elements

bool equals ( const Matrix &  a  )  const

bytewise comparison (compares data buffer bytewise, which implies that n1*m1 == n2*m2 but not necessarily n1==n2)

void exp ( const Matrix &  a,
int  exponent 
)

exponent, this = a^i,

See also:
toExp
I getM (  )  const [inline]
Returns:
number of rows
I getN (  )  const [inline]
Returns:
number of columns
bool hasNormalEntries (  )  const

returns true if all entries are normal floating point numbers, otherwise false (e.g.

for nan and inf)

bool isNulltimesNull (  )  const

returns true if matrix is a 0x0 matrix

ACCESSORS ///////////////////////////////////////////////////////////////.

bool isVector (  )  const

returns true if matrix is a vector

Matrix map ( D(*)(D)  fun  )  const

maps the matrix to a new matrix with all elements mapped with the given function

Examples:
matrix/matrixexample.cpp.
Matrix map2 ( D(*)(D, D)  fun,
const Matrix &  a,
const Matrix &  b 
) [static]

binary map operator for matrices.

The resulting matrix consists of the function values applied to the elements of a and b. In haskell this would something like: map (uncurry . fun) $ zip a b

Matrix map2P ( void *  param,
D(*)(void *, D, D)  fun,
const Matrix &  a,
const Matrix &  b 
) [static]

like map2P but with arbitrary paramters (void*) instead of double

Matrix map2P ( D  param,
D(*)(D, D, D)  fun,
const Matrix &  a,
const Matrix &  b 
) [static]

like map2 but with additional parameter.

The first argument of fun is the parameter and the second and third comes from the matrix elements. In haskell this would something like: map (uncurry . (fun p)) $ zip a b

Matrix mapP ( void *  param,
D(*)(void *, D)  fun 
) const

like map but with additional arbitrary parameter for the mapping function

Matrix mapP ( D  param,
D(*)(D, D)  fun 
) const

like map but with additional double parameter for the mapping function (first argument of fun is parameter, the second is the value)

void mult ( const Matrix &  a,
const D &  fac 
)

scaling: this = a * fac

void mult ( const Matrix &  a,
const Matrix &  b 
)

multiplication: this = a * b

Matrix multcolwise ( const Matrix &  factors  )  const

column-wise multiplication

Parameters:
factors column vector (Mx1) of factors, one for each column
Matrix multMT (  )  const

optimised multiplication of Matrix with its transposed: M * M^T

Matrix multrowwise ( const Matrix &  factors  )  const

row-wise multiplication

Parameters:
factors column vector (Mx1) of factors, one for each row
Examples:
matrix/matrixexample.cpp.
Matrix multTM (  )  const

optimised multiplication of transpsoed of Matrix with itself: M^T * M

D norm_sqr (  )  const

returns the sum of all squares of all elements (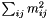$ \sum_{ij} m_{ij}^2 $) this is also known as the square of the Frobenius norm.

returns the sum of all elements

Matrix operator& ( const Matrix &  b  )  const

row-wise multiplication

Matrix& operator&= ( const Matrix &  c  )  [inline]

combined assigment operator (higher performance)

Matrix operator* ( const D &  fac  )  const

product with scalar (D) (only right side)

product with scalar (double)

Matrix operator* ( const Matrix &  fac  )  const

matrix product

Matrix& operator*= ( const D &  fac  )  [inline]

combined assigment operator (higher performance)

Matrix& operator*= ( const Matrix &  c  )  [inline]

combined assigment operator (higher performance)

Matrix operator+ ( const Matrix &  sum  )  const

sum of two matrices

Matrix& operator+= ( const Matrix &  c  )  [inline]

combined assigment operator (higher performance)

Matrix operator- ( const Matrix &  sum  )  const

difference of two matrices

Matrix& operator-= ( const Matrix &  c  )  [inline]

combined assigment operator (higher performance)

Matrix& operator= ( const Matrix &  c  )  [inline]

deep copy

bool operator== ( const Matrix &  c  )  const

comparison operator (compares elements with tolerance distance of COMPARE_EPS)

Matrix operator^ ( int  exponent  )  const

special matrix potence:

Parameters:
exponent -1 -> inverse; 0 -> Identity Matrix; 1 -> itself; T -> Transpose
exp -1 -> inverse; 0 -> Identity Matrix; 1 -> itself; 2-> Matrix*Matrix^T T -> Transpose
Matrix & pluslambdaI ( double  lambda = 1e-8  ) 

adds the given value to the diagonal

Matrix pseudoInverse ( const D &  lambda = 1e-8  )  const

calculates the pseudoinverse, depending on the shape of the matrix the left or right pseudoinverse is used.

If the matrix has more columns than rows then we use

\[A^{+} = (A^T A + \lambda \mathbb I)^{-1}A^T\]

otherwise

\[A^{+} = A^T(A A^T + \lambda \mathbb I)^{-1}\]

bool read ( FILE *  f  ) 

reads a Matrix from the given file stream (ascii)

Matrix & removeColumns ( I  numberColumns  ) 

removes one or more columns of the existing matrix resets the size of the matrix and deletes the appropiate data.

Parameters:
numberColumns number of columns to remove (this reduces n)
Returns:
the address of the matrix itself
Matrix & removeRows ( I  numberRows  ) 

removes one or more rows of the existing matrix, same as reshape(getM()-numberRows, getN());

Parameters:
numberRows number of rows to remove (this reduces m)
Returns:
the address of the matrix itself
Matrix & reshape ( I  m,
I  n 
)

reshapes the matrix without destroying the data.

Remember: The data is stored rowwise.

Only shrinking is allowed i.e. m*n must be lower or equal to getM()*getN()

bool restore ( FILE *  f  )  [virtual]

reads a Matrix from the given file stream (binary)

Implements Storeable.

Matrix row ( I  index  )  const
Returns:
row-vector(as 1xN matrix) containing the index'th row
Examples:
matrix/matrixexample.cpp.
Matrix rows ( I  startindex,
I  endindex 
) const
Returns:
submatrix (as KxN matrix) containing row from startindex to endindex inclusively (K=stopindex-endindex) indices can be out of bounds, they are clipped in any case
Matrix secureInverse (  )  const

calculates the secure inverse of a square matrix.

If singular then the pseudoinverse is used.

void set ( const D *  _data  ) 

sets the data (row-wise).

Parameters:
_data if null then matrix elements are set to zero otherwise the field MUST have the length should be getM()*getN()
void set ( I  _m,
I  _n,
const D *  _data = 0 
)

sets the size of the matrix and maybe the data if given (row-wise).

If data=null then the matrix is set to zero

See also:
toZero()
constructor Matrix(m,n,data)
Examples:
matrix/matrixexample.cpp.
I size (  )  const [inline]
Returns:
number number elements in the matrix (getM()*getN())
bool store ( FILE *  f  )  const [virtual]

stores the Matrix into the given file stream (binary)

Implements Storeable.

void sub ( const Matrix &  a,
const Matrix &  b 
)

add scalar to each element

subtraction: this = a - b

Matrix & toAbove ( const Matrix &  a  ) 

sets the matrix a below this matrix

Matrix & toBeside ( const Matrix &  a  ) 

sets the matrix a right beside this matrix

Matrix & toDiff ( const Matrix &  a  ) 

inplace subtraction: this = this - a

Matrix & toExp ( int  exponent  ) 

special inplace matrix power:

Parameters:
exponent -1 -> inverse; (matrix MUST be SQUARE and NONZERO) 0 -> Identity Matrix; 1 -> itself; n -> n-th power; T -> Transpose
Matrix & toId (  ) 

inplace converts matrix to identity (use ^0 to get a copy version of it)

Examples:
integration/main.cpp.
Matrix & toMap ( D(*)(D)  fun  ) 

inplace mapping of matrix elements (element-wise application)

Matrix & toMap2 ( D(*)(D, D)  fun,
const Matrix &  b 
)

like toMap, but with using 2 matrices

Matrix & toMap2P ( void *  param,
D(*)(void *, D, D)  fun,
const Matrix &  b 
)

like toMap2P, but with arbitrary parameter

Matrix & toMap2P ( D  param,
D(*)(D, D, D)  fun,
const Matrix &  b 
)

like toMap2, but with additional parameter

Matrix & toMapP ( void *  param,
D(*)(void *, D)  fun 
)

like toMap, but with an extra arbitrary parameter for the mapping function.

Matrix & toMapP ( D  param,
D(*)(D, D)  fun 
)

like toMap, but with an extra double parameter for the mapping function.

Matrix & toMult ( const D &  fac  ) 

inplace multiplication with scalar: this = this*fac

Matrix & toMult ( const Matrix &  a  ) 

inplace multiplication: this = this * a

Matrix & toMultcolwise ( const Matrix &  factors  ) 

Inplace column-wise multiplication.

Parameters:
factors column vector of factors, one for each column
Matrix & toMultrowwise ( const Matrix &  factors  ) 

Inplace row-wise multiplication.

Parameters:
factors column vector of factors, one for each row
Matrix & toSort (  ) 

sorts the matrix (rowwise)

Matrix & toSum ( const D &  sum  ) 

inplace addition: this = this + a, where a is a scalar

Matrix & toSum ( const Matrix &  a  ) 

inplace addition: this = this + a

Matrix & toTranspose (  ) 

inplace transpose

Matrix & toZero (  ) 

inplace converts matrix to zero matrix

const double* unsafeGetData (  )  const [inline]

returns a pointer to the data. UNSAFE!!!

D& val ( I  i,
I  j 
) [inline]
Returns:
reference to element at position i,j (can be used as left side value)
D val ( I  i,
I  j 
) const [inline]
Returns:
element at position i,j (row, column index)
Examples:
matrix/matrixexample.cpp.
D valDef0 ( I  i,
I  j 
) const [inline]
Returns:
element at position i,j (row, column index) and 0 if out of bounds
bool write ( FILE *  f  )  const

writes the Matrix into the given file stream (ascii)

Friends And Related Function Documentation

std::ostream& operator<< ( std::ostream &  str,
const Matrix &  mat 
) [friend]

printing operator: output format: mxn (
row0
..rown
) where rowX is tab seperated list of values

The documentation for this class was generated from the following files:
Generated on Thu Jun 28 14:49:08 2012 for Robot Simulator of the Robotics Group for Self-Organization of Control by  doxygen 1.6.3